Turing Omnibus #1: Algorithm for generating wallpapers

I have started to read The New Turing Omnibus - a book that offers 66 concise, brilliantly written articles on the major points of interest in computer science theory, technology and applications.

From time to time, I will write a blog post presenting a chapter of this book.

omnibus

Today, I am glad to present an interactive version of Chapter 1 about algorithms in general.

The algorithm

In order to explain what is an algorithm, the author presents a simple recipe for generating wallpapers.

Here is the recipe:

algo

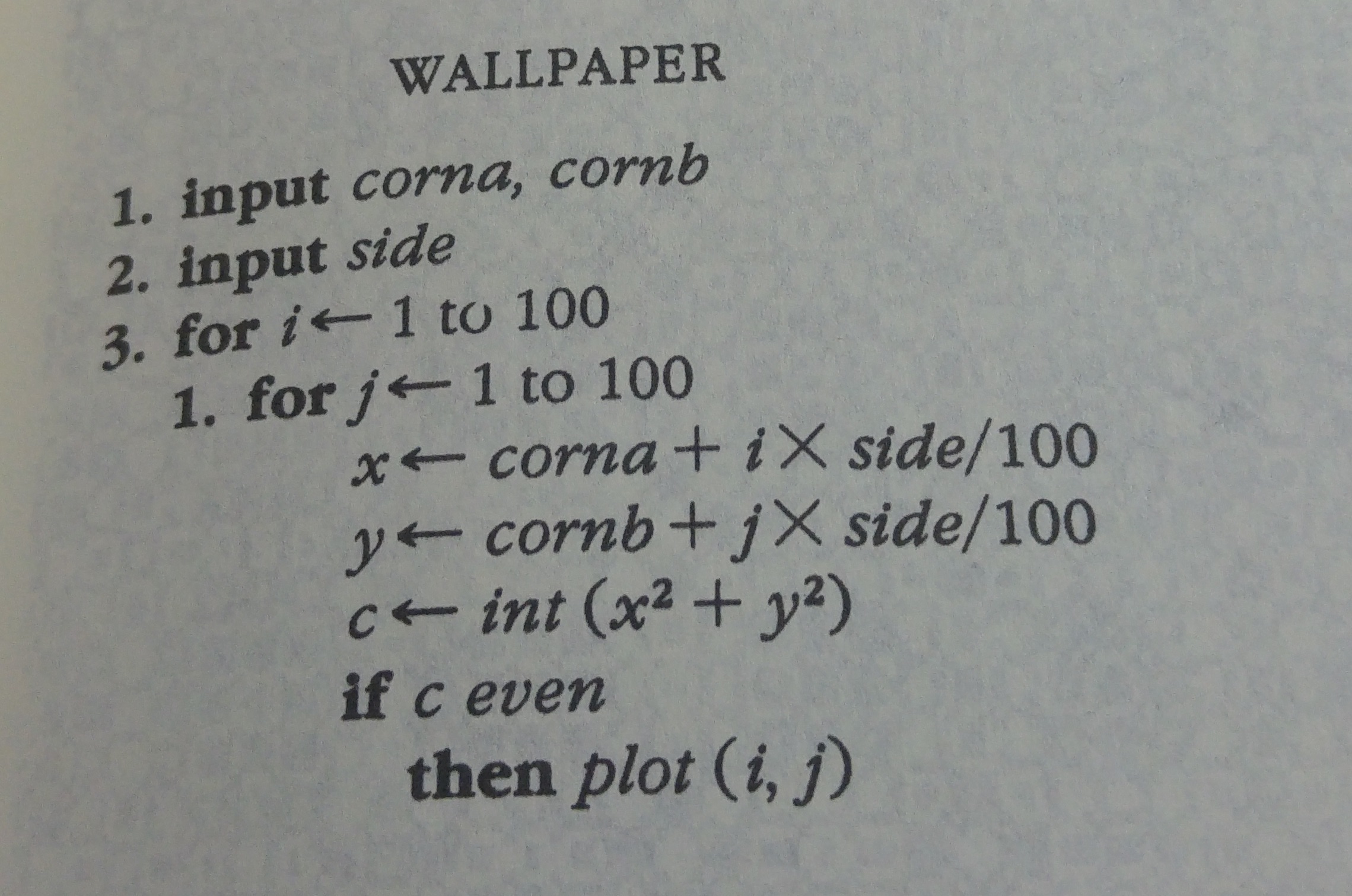
Now, we are going to code this algorithm in Clojurescript and you will be able to play with it in your browser thanks to the interactive Klipse snippets.

Preliminaries

First, we need a function that draws a color pixel on a canvas:

(defn draw-pixel! [canvas x y color]
  (let [ctx (.getContext canvas "2d")
        scale 2]
    (set! (.-fillStyle ctx) color)
    (.fillRect ctx (* scale x) (* scale y) scale scale)))

Then, a function that erases a canvas i.e. color it in white:

(defn reset-canvas! [canvas]
(let [ctx (.getContext canvas "2d")]
  (set! (.-fillStyle ctx) "white")
  (.fillRect ctx 0 0 (.-width canvas) (.-height canvas))))

Black and White Wallpaper

The algorithm is controlled by the geometry of a square:

its x-position named a
its y-position named b
the side of the square named side



(defn draw-bw-wallpaper! [canvas a b side]
  (let [points 200]
  (dotimes [i points]   
    (dotimes [j points]
      (let [x (+ a (* i (/ side points)))
            y (+ b (* j (/ side points))) 
            c (int (+ (* x x) (* y y)))] 
        (when (even? c)
          (draw-pixel! canvas i j "black")))))))

(draw-bw-wallpaper! canvas 5 5 9)

The cool thing about this algorithm is that when we modify the side of the square, we get a completly different pattern:


(draw-bw-wallpaper! canvas 5 5 100)

Go ahead, play with the code…

The interactive code snippets are powered by the Klipse plugin.

Three Colors

We can generate a 3-color wallpaper by calculating the remainder of c modulo 4 and chose a color accordingly:



(defn draw-color-wallpaper! [canvas a b side]
  (let [points 200]
    (dotimes [i points]
      (dotimes [j points]
        (let [x (+ a (* i (/ side points)))
              y (+ b (* j (/ side points)))
              c (int (+ (* x x) (* y y)))
              color  (case (mod c 4)
                       0 "red"
                       1 "green"
                       2 "blue"
                       "white")]
         (draw-pixel! canvas i j color))))))

(draw-color-wallpaper! canvas 5 7 101)

Again, when we modify the side of the square, we get a completly different pattern:


(draw-color-wallpaper! canvas 5 7 57)

Grand Finale

Someone in reddit suggested to loop over the value of side in order to watch all the generated wallpapers like a movie.

Here is the result:


(defonce interval (atom nil))
(defonce side (atom 0))

(def delta 0.5)
(defn step [canvas container]
  (set! (.-innerHTML container) (str "side: " @side) )
  (reset-canvas! canvas)
  (draw-color-wallpaper! canvas 5 5 (swap! side + delta)))

(.clearInterval js/window @interval)
(reset! side 0)
(reset! interval (.setInterval js/window step  500 canvas js/klipse-container))

Are you able to provide a simple explanation about this algorithm?

How is it able to generate so many different beautiful patterns?

Have you found a magnificient pattern? Please share its code…

Yehonathan Sharvit